Aby rozwiązać rozważany problem, można zastosować następujące metody, z których każda ma swoje zalety i wady.
Metoda wyliczania określonych opcji rozwoju CHP. W tej metodzie, opierając się na intuicji i doświadczeniu inżynierskim specjalisty, tworzone są możliwe opcje dotyczące składu i czasu wprowadzania turbin wytwarzających ciepło, a dla każdego z nich określa się optymalną liczbę i warunki instalacji kotłów energetycznych, szczytowych kotłów parowych i ciepłej wody. Wybór ostatecznej decyzji jest dokonywany na podstawie porównania opcji uwzględnionych przy minimalnych obniżonych kosztach. Zaletami metody sortowania danych opcji dla rozwoju CHP są: prostota, wygoda użycia w praktyce inżynierskiej, stosunkowo mała złożoność obliczeń, ograniczony zakres poszukiwania optymalny. Jednak ta metoda nie gwarantuje uzyskania prawdziwie optymalnego rozwiązania, ponieważ obliczenia uwzględniają tylko niewielką część możliwych opcji pod względem składu i harmonogramu uruchomienia głównego sprzętu CHP.
Metoda kombinatoryczna. W przypadku zastosowania tej metody, dla każdego okresu obliczeniowego ustalonego dla ostatniego roku wariantu, zgodnie ze składem turbin grzewczych, tworzona jest algorytmiczna formuła możliwych opcji dla rozwoju elektrociepłowni.

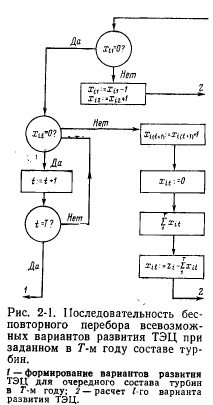
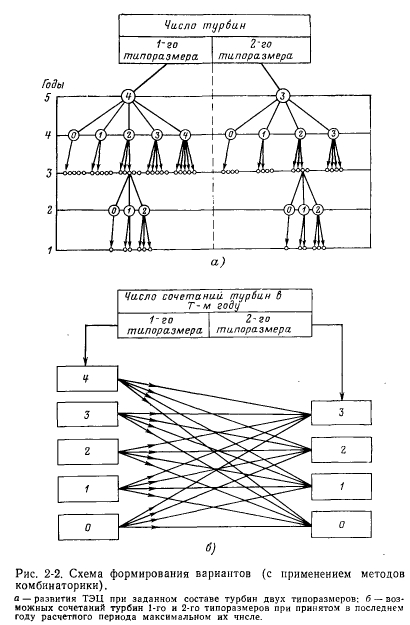
Sekwencja tworzenia opcji dla składu i czasu wprowadzania głównego sprzętu dla bardziej złożonego przypadku, gdy turbiny o dwóch rozmiarach są instalowane w elektrociepłowniach, wyjaśnia schemat na ryc. 2-2, w górnej części której znajduje się schemat tworzenia opcji wprowadzania turbin grzewczych pierwszej i drugiej wielkości, począwszy od ostatniego roku okresu rozliczeniowego. Uwzględniono wówczas 5 lat i przyjęto liczbę turbin równą odpowiednio 4 i 3. Kropki w tych konstrukcjach wskazują teoretycznie dopuszczalne sposoby przejścia z następnego roku na poprzedni, ale praktycznie niemożliwe przy rozwiązywaniu tego zadania, ponieważ liczba turbin, na przykład, w 4 roku nie może być mniejsza niż w trzecim roku. W dolnej części rys. 2-2 schematycznie przedstawia zasadę tworzenia wariantów kombinacji turbin pierwszej i drugiej wielkości w T-tym roku dla danej maksymalnej liczby. Dla każdej z tych kombinacji „rozwiertak” jest wytwarzany zgodnie ze schematem wskazanym w górnej części rys. 2-2, tj. Możliwe opcje są określane przez czas wprowadzania turbin dla danego wariantu ich składu w ostatnim roku okresu obliczeniowego.
Zalety nie powtarzającej się metody badania możliwości rozwoju CHP obejmują: 1) określenie całego zakresu rozwiązań i na podstawie jego analizy - rzeczywiste optimum; 2) mniej pracochłonny w porównaniu z poprzednią metodą przy przygotowywaniu wstępnych informacji do obliczeń komputerowych; 3) możliwość przetestowania stabilności optymalnego rozwiązania przy zmianie danych źródłowych.
Jednak powszechne stosowanie tej metody jest trudne ze względu na konieczność iteracji dużej liczby opcji rozwoju CHP (L), która znacznie wzrasta wraz z wydłużaniem się okresu rozliczeniowego i liczbą rozmiarów turbin grzewczych. Wartość L dla danej liczby turbin pierwszej wielkości Zi i drugiej wielkości Z2 w zależności od liczby lat T może być określona przez wyrażenie [55, 71]
Na przykład, gdy Zi = 3 i Z2 = 0, teoretycznie możliwa liczba opcji rozwoju CHP wynosi 35 przy T = 5 lat i 220 przy 7 = 10 lat. Oczywiście, taka liczba opcji rozwoju CHP jest teoretycznie możliwa. W rzeczywistości większość z nich będzie nie do przyjęcia ze względów inżynieryjnych, a biorąc pod uwagę te rozważania w postaci odpowiednich ograniczeń zapisanych w programie obliczeniowym, może nie zostać uwzględniona. Ograniczenia te obejmują: 1) możliwą maksymalną kombinację liczby turbin pierwszego i drugiego rozmiaru dla danej wartości i struktury obciążeń termicznych; 2) maksymalną liczbę turbin, które można wprowadzić w CHP w ciągu jednego roku; 3) dopuszczalne luki w czasie wprowadzania pierwszej i kolejnych turbin w okresie rozliczeniowym itp.
Jednakże, ponieważ analiza wykazała, nawet w tych warunkach, obliczenie wszystkich możliwości rozwoju elektrowni kogeneracyjnych, które są dopuszczalne ze względów inżynierskich, stwarza duże trudności w korzystaniu z komputera klasy średniej (typ BESM-4).
Dynamiczna metoda programowania. Podczas korzystania z tej metody przeprowadzane jest ukierunkowane wyszukiwanie możliwych opcji, ich liczba drastycznie maleje, a wybór optymalnego składu i czasu uruchomienia urządzeń kogeneracyjnych jest gwarantowany. Podstawową zasadą, z której wynika, jest podział złożonego zadania na szereg kolejnych etapów (kroków). W rezultacie proces rozwiązywania problemu staje się wieloetapowy, w którym rozwiązanie jest optymalizowane tylko na każdym etapie, ale z uwzględnieniem wszystkich możliwych rozwiązań
Metoda programowania dynamicznego ma zastosowanie, gdy spełnione są następujące główne warunki: 1) funkcja, która ma być zoptymalizowana, jest addytywna, tj. Jest sumą składników tego samego rodzaju we wszystkich etapach procesu optymalizacji, co umożliwia zastąpienie poszukiwania optymalności funkcji wielu zmiennych wieloma definicjami krok) optimum małej ich liczby; 2) decyzja podjęta na tym etapie zależy od poprzedniego stanu obiektu energetycznego (systemu) i nie zależy od jego późniejszego stanu. Potrzeba spełnienia tych warunków naturalnie wpływa na możliwość zastosowania rozważanej metody do wielu zadań w energetyce. Jednocześnie przyciąga swoimi zaletami: znaczne zmniejszenie wymiaru problemu; umiejętność rozwiązywania problemów nie za pomocą pojedynczego ekstremum, dyskretnej zmiany zmiennych itp. Wyjaśnia to chęć rozszerzenia obszaru stosowania metody programowania dynamicznego, w tym rozwiązania niektórych problemów optymalizacji elektrowni cieplnych [33].
Należy zauważyć, że dla tej metody nie ma standardowych metod formułowania problemu, wyboru podstawowych zmiennych, organizacji procesu krok po kroku rozwiązania. W każdym konkretnym przypadku wymagane jest uzasadnienie możliwości jego zastosowania, a także kolejność rozwiązywania rozważanego problemu.
Aby zoptymalizować skład i czas wprowadzania głównego wyposażenia elektrociepłowni, można zastosować metodę programowania dynamicznego z jednym niezbędnym założeniem: koszt turbin grzewczych, kotłów, szczytowych kotłów parowych i ciepłej wody nie zależy od czasu ich instalacji w elektrociepłowni. Oczywiście w rzeczywistości może się to nieznacznie zmienić, zwłaszcza gdy sprzęt jest rozproszony, ponieważ w tym przypadku wzrosną koszty związane z wykorzystaniem mechanizmów wykorzystywanych przy budowie elektrociepłowni, siły roboczej itp. Aby ocenić stopień wpływu tych czynników na koszt podstawowego sprzętu Wymagana jest specjalna analiza rzeczywistych i regulacyjnych wskaźników budowy poszczególnych elektrociepłowni.
Jeśli weźmiemy pod uwagę odnotowane założenie, funkcję celu, czyli obniżone koszty CHP, można uznać za dodatek. Rzeczywiście, koszty obejmują koszty inwestycyjne i operacyjne dla każdego roku i koszt roku normalnej eksploatacji. Ponieważ wydatki kapitałowe muszą być obliczane oddzielnie dla każdego roku, cały proces określania obniżonych kosztów naturalnie przypada na T kroków, które są od siebie niezależne. W ten sposób spełnione są powyższe wymagania, które pozwalają na zastosowanie dynamicznej metody programowania do rozwiązania problemu. W każdym kolejnym roku liczba turbin nie może być mniejsza niż liczba turbin z poprzedniego roku - realizacja tego ograniczenia nie oznacza uzależnienia obniżonych kosztów kolejnego roku od kosztów poprzedniego, ponieważ w przyszłym roku można wprowadzić kilka turbin jednocześnie lub bez, niezależnie od jakie koszty są związane z poprzednim rokiem. Koszty są ustalane dla optymalnego wariantu w i-tym roku, a następnie sumowane z kosztami dla wariantu wybranego w (t— 1) roku.
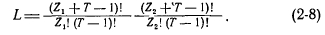
W tym zadaniu w każdym roku okresu obliczeniowego można wprowadzić określoną liczbę całkowitą turbin lub nie. W tym przypadku turbiny mogą mieć jeden rozmiar lub dwa rozmiary. W przypadku elektrowni cieplnych z turbinami o tej samej wielkości proces rozwoju przedstawiono schematycznie na rys. 2-3. Oto „siatka”, której punkty są uzyskiwane przez przecięcia linii poziomych charakteryzujących liczbę turbin grzewczych o tym samym rozmiarze i linie pionowe określające liczbę lat okresu obliczeniowego.
Kolejność rozwiązywania problemu. Zgodnie z opracowanym algorytmem opartym na wykorzystaniu programowania dynamicznego zadanie optymalizacji składu i czasu uruchomienia urządzeń CHP rozwiązuje się w następującej kolejności:
1. Na podstawie maksymalnej liczby turbin pierwszego i drugiego rozmiaru określonych dla ostatniego roku okresu obliczeniowego, tworzona jest następna wersja ich składu i możliwe opcje rozwoju CHP są określane przez algorytm programowania dynamicznego.
2. Dla każdego ukształtowanego wariantu rozwoju CHP określa się:
dla każdego z T lat: a) roczna dostawa ciepła z wybranych turbin o określonych rozmiarach standardowych, przez DOW oraz z szczytowych kotłów parowych i gorącej wody; b) wytwarzanie energii elektrycznej na zużycie ciepła i na tryb kondensacji; roczne zużycie paliwa przez kotły energetyczne i szczytowe; koszty kapitałowe i operacyjne;
za okres T lat: zużycie paliwa przez kotły energetyczne i szczytowe, inwestycje kapitałowe, koszty operacyjne i obniżone koszty.
3. W wyniku wyliczenia możliwych opcji rozwoju CHP, gdy zostanie określony skład turbin pierwszej i drugiej wielkości określonych w T, najlepsze rozwiązanie jest ustalane i wydawane do druku (dla okresu rozliczeniowego): daty uruchomienia turbin o podanych rozmiarach, skład i kolejność instalacji energii, szczytowa para i kotły wodne; zużycie paliwa przez kotły energetyczne i szczytowe, inwestycje, eksploatację i obniżone koszty.
4. Utworzono w roku T nową wersję składu turbin pierwszej i drugiej wielkości, a obliczenia wykonuje się w podobnej kolejności. Proces obliczeniowy trwa, dopóki wszystkie opcje nie zostaną skompilowane i obliczone pod względem składu i czasu wprowadzania głównego wyposażenia CHP. W wyniku takich obliczeń ustalane jest optymalne rozwiązanie dla rozwoju elektrowni kogeneracyjnej.
Na rys. 2-5 schematycznie przedstawiają kolejność rozwiązania problemu wyboru dla CHP końcowego składu i kolejności uruchamiania turbin wytwarzających ciepło, mocy, szczytowej pary i kotłów z gorącą wodą. Konstrukcje te są wykonane dla bardziej złożonego przypadku, gdy turbiny typu T i P o różnej wydajności jednostkowej są wprowadzane przy mieszanym obciążeniu cieplnym elektrociepłowni.
Przy rozwiązywaniu problemu, dla każdego wariantu rozwoju elektrociepłowni w piątym roku okresu obliczeniowego, wytwarza się: a) doprowadzenie opcji do jednakowego efektu energetycznego; b) optymalny rozkład obciążenia regulowanej ekstrakcji turbin wytwarzających ciepło; c) określanie liczby kotłów energetycznych, szczytowych pary i gorącej wody; d) obliczanie wskaźników technicznych i ekonomicznych CHP.
Poniżej rozważane są te etapy obliczeń przy rozwiązywaniu problemu wyboru optymalnego składu i harmonogramu wejścia do głównego wyposażenia elektrowni cieplnych dla bardziej skomplikowanego przypadku - w obecności mieszanego obciążenia cieplnego, w tym zużycia ciepła, dla technologii, ogrzewania i zaopatrzenia w ciepłą wodę.

Zbliżanie charakterystyk turbin grzewczych. W procesie rozwiązywania omawianego problemu, zwłaszcza gdy turbiny z dwoma regulowanymi wyborami i kondensacją pary wodnej są instalowane na elektrociepłowniach, konieczne staje się określenie zależności zmian ich parametrów, w szczególności: zużycia ciepła do turbiny QT od jego mocy elektrycznej Nt i mocy cieplnej z pierwszego Qi i drugiego Wybór Qn; dostarczanie ciepła z pierwszego kontrolowanego wyboru z podanych wartości QT, Nt i Qn; dostawa ciepła z drugiego kontrolowanego wyboru przy stałych wartościach QT, Qi;
zużycie pary na turbinę na wartość QT, a także szereg innych zależności, które zostaną omówione poniżej.
Charakterystyczną cechą tych zależności jest monotonia i gładkość zmiany, która umożliwia zastosowanie wielomianu do ich przybliżonego opisu, którego ekspresję można znaleźć metodą najmniejszych kwadratów [371.

Zatem znalezienie współczynników najlepszego wielomianu aproksymacyjnego sprowadza się do rozwiązania układu równań liniowych, co można zrobić za pomocą odpowiednich standardowych programów. Dokładność aproksymacji wielomianu zależy od typu funkcji przybliżającej, stopnia wielomianu, liczby punktów pobranych do aproksymacji itp. Średni błąd względny aproksymacji można obliczyć z wyrażenia
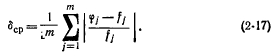
Jak pokazały obliczenia, powyższe zależności mogą być reprezentowane z wystarczającym stopniem dokładności przez wielomiany trzeciego rzędu.
Metoda doprowadzania opcji rozwoju CHP do równego efektu energetycznego. W rozdz. 1 omawia ogólne zasady doprowadzania różnych wariantów systemu dostarczania ciepła do jednakowego efektu energetycznego. W tym przypadku, optymalizując rozwój CHP, zasady te przybierają bardziej konkretną formę, która wygląda następująco.
Proponowana metoda polega na porównaniu dużej liczby opcji, które różnią się składem i czasem wejścia głównego sprzętu, lub tylko w czasie wprowadzania głównego wyposażenia CHP. Dlatego, dla porównywalności, wszystkie rozważane warianty powinny zostać zredukowane do równego efektu energetycznego zarówno pod względem mocy elektrycznej, jak i wytwarzania energii elektrycznej. Wśród porównywanych opcji uwzględniono również, w których wszystkie turbiny są wprowadzane w elektrociepłowni w pierwszym roku okresu rozliczeniowego, ze wzrostem obciążenia cieplnego w przód, a zatem moc elektryczna CHP jest taka sama przez cały okres rozliczeniowy. W związku z tym wszystkie porównywane opcje muszą być doprowadzone do stałej przez cały okres zasilania elektrycznego. Oczywiste jest, że wartość tej mocy, zwanej dalej „mocą podstawową”, nie może być mniejsza niż w wariancie CHP o maksymalnej mocy elektrycznej. Maksymalne wytwarzanie energii przy stałej mocy elektrycznej CHP zostanie osiągnięte przy maksymalnej dostawie ciepła z CHP, tj. W ostatnim roku rozpatrywanego okresu.
W związku z tym w przypadku opcji dotyczących składu turbin grzewczych określonych dla ostatniego roku okresu obliczeniowego określa się całkowitą moc elektryczną elektrociepłowni MW:
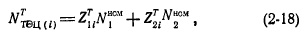
Zmniejszenie porównywanych opcji rozwoju CHP do równego efektu energetycznego odbywa się poprzez uwzględnienie uzupełniającej mocy [M> .0 (i)] i wytwarzanie energii elektrycznej w systemie elektroenergetycznym (ES). W tym przypadku w podstawowej wersji M ».c (i) i W9.cu) przyjmowane są równe 0.
Ponieważ rozważa się budowę nowej elektrociepłowni, wyklucza się demontaż sprzętu w rozważanym okresie (10–15 lat). Dlatego można założyć, że moc elektryczna elektrociepłowni i wytwarzanie na niej energii elektrycznej pozostają stałe lub rosną. Wynika z tego, co należy wziąć pod uwagę w obliczeniach, gdy przechodzimy od (t - 1) roku do i-tego, albo pozostaniemy na stałym poziomie albo spadamy, a przyrost zastępowanej mocy w dowolnym roku, z wyjątkiem tego, że pierwszy jest równy lub mniejszy niż 0 Wzrost Ng.c) w i-tym roku wyniesie, MW:


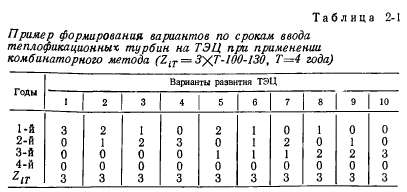
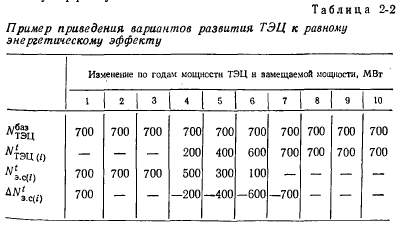
Jak wspomniano powyżej, podstawową moc CHP w całym okresie T lat przyjmuje się jako stałą. Dlatego jego wzrost w pierwszym roku okresu może być równy jego wartości bezwzględnej oraz w dowolnym innym roku. Tak więc przyrost zdolności uzupełniającej w ES w każdym roku innym niż pierwszy jest równy wzrostowi mocy CHP w tym samym roku ze znakiem przeciwnym. Jednak dla jednolitości obliczeń wartość L jest określona przez wyrażenie (2-19). Ilustracje w tabeli. 2-2 przedstawia przykład wprowadzenia opcji rozwoju CHP na równy efekt energetyczny.

Tak więc, redukując opcje, które różnią się składem i czasem wprowadzenia głównego wyposażenia elektrociepłowni, do jednakowego efektu energetycznego, konieczne jest przeanalizowanie stosunków wytwarzania energii elektrycznej i energii elektrycznej w każdym roku okresu rozliczeniowego. Dla danej serii lat wskaźniki te mogą się różnić (w porównaniu z ich wartościami bazowymi), a zatem wartość konkretnych kosztów zamknięcia energii elektrycznej musi być również traktowana jako zmienna.
Optymalna moc pobierana z turbiny do ekstrakcji ciepła. Zadanie wyboru optymalnego obciążenia kadłuba przy instalacji na elektrociepłowni z turbinami PT o dwóch typach (Rys. 2-6). Górny regulowany wybór tych turbin jest wykorzystywany do dostarczania ciepła do celów technologicznych Naturalnie, w zależności od wybranej selekcji, wydajności turbin rozpatrywanego rozmiaru ulegnie zmianie. Do oceny wykorzystujemy metodę charakterystyk energetycznych [43, 66], wyrażającą zależność między zużyciem ciepła Q dostarczanym do turbiny a elektrycznym N, jak również obciążeniami termicznymi QT, tj.


Roczne zużycie ciepła dla turbiny kogeneracyjnej Qr ° a oraz roczne wytwarzanie energii elektrycznej przy zużyciu ciepła Wm i przez tryb kondensacji WK z wykorzystaniem metody charakterystyki energetycznej określają następujące wyrażenia:

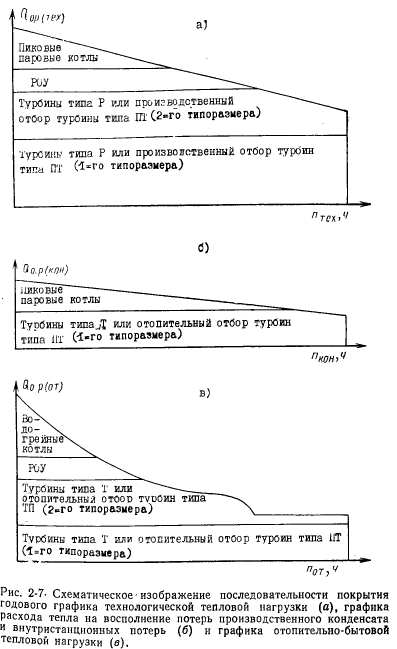
W oparciu o metodę charakterystyki energetycznej „turbiny cieplne” są „umieszczane” w rocznych wykresach obciążenia cieplnego przez czas trwania. Podstawowy charakter schematów obciążeń technologicznych, zużycie ciepła do uzupełnienia zewnętrznych i wewnętrznych strat ciepła i obciążenia cieplnego ogrzewania domowego podano na rys. 2-7. Szacowane godzinowe wyładowania ciepła z wyboru produkcji i ogrzewania turbiny PT są ze sobą powiązane: ich wartości pochodzą z warunku osiągnięcia najwyższego wytwarzania energii w trybie wytwarzania ciepła. Ten warunek jest następujący. Oznaczmy stosunek godzinowego uwolnienia ciepła z wyboru „produkcji” (Q1) do całkowitej dostawy ciepła z wyborów (QI + n): 
Biorąc pod uwagę wartość współczynnika podanego w t-tym roku, godzinowe i roczne dostawy ciepła dla celów technologicznych i ogrzewania domowego są określane dla turbin pierwszego rozmiaru. Uwzględniono następujące ograniczenia i warunki:
1. Szacowany współczynnik dostarczania ciepła nie powinien przekraczać maksymalnej wartości równej

Przy określaniu bierze się pod uwagę ogólnie przyjętą pozycję początkową, przy której obciążenie cieplne elektrociepłowni uważa się za podane, a jej moc elektryczna jest zmienną [43]. Najwyraźniej, w niektórych przypadkach, zwłaszcza przy znacznym wzroście mocy elektrowni kondensacyjnych na podstawie wykresu obciążenia elektrycznego, co prowadzi do ograniczenia mocy elektrycznej CHP, mogą zostać stworzone warunki wstępne, w których wybór optymalnej wartości będzie bardziej efektywny przy produkcji Q0.p = var i 3 Nrm = const. W zasadzie wyznanie. N. I. Dunaevsky [17].
2. Turbiny powinny pracować z wiązką generującą ciepło zawartą w skraplaczu.
Po określeniu rocznego zaopatrzenia w ciepło z turbin pierwszego rozmiaru, są one obliczane (na podstawie metody charakterystyki energetycznej) rocznej produkcji energii elektrycznej w trybie wytwarzania ciepła, MWh:

Wartości tych wielkości dla turbin PT-60-130 i PT-135-130, w zależności od współczynnika f (g ° E), pokazano na rys. 2-8.
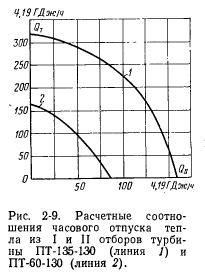
Ustalając wartość Wm (IT), wartość znaleziona przy współczynniku Pi idzie do optymalnej redystrybucji dostaw ciepła z wyboru turbiny PT drugiego rozmiaru. Biorąc pod uwagę współczynnik, wyznaczają one całkowitą obliczoną dostawę ciepła z dwóch selekcji turbin Т z drugiego standardowego rozmiaru О do niego obliczonego zaopatrzenia w ciepło z pierwszego (Q2m) drugiego wyboru Qgj. Zależność turbin PT-60-130 i PT-135-130 jest graficznie przedstawiona na ryc. 2-9.
Biorąc pod uwagę podane ograniczenia wartości obliczonego obciążenia cieplnego ciepła technologicznego i krajowego w t-tym roku, obliczane są rzeczywiste godzinowe i roczne uwolnienia ciepła z turbin drugiego rozmiaru. Następnie generowanie energii elektrycznej przez tryb generowania ciepła przez te turbiny W'm (2 /} może być określone przez wyrażenie podobne do (2-31).
Przy optymalizacji obciążenia regulowanych wyborów turbin typu sizesT pierwszej i drugiej wielkości przyjmuje się kryterium osiągnięcia największej całkowitej produkcji energii elektrycznej w trybie wytwarzania ciepła przez te turbiny Wlm (X).
W oparciu o ten warunek optymalne rozwiązanie można znaleźć za pomocą metody opartej na użyciu szeregu liczb Fibonacciego [11]. Gdy okaże się, że optymalne rozwiązanie znalezione za pomocą tej metody jest ustalone, wartości wytwarzania energii elektrycznej w trybie wytwarzania ciepła przez turbiny pierwszego i drugiego rozmiaru. Wtedy wytwarzanie energii elektrycznej w trybie kondensacji będzie: dla turbin pierwszego rozmiaru, MWh:

Określenie liczby kotłów energetycznych, szczytowych pary i gorącej wody w CHP. Wybór liczby tych kotłów jest przeprowadzany w celu zapewnienia produkcji energii elektrycznej i cieplnej w wymaganych rozmiarach w elektrociepłowniach. W tym przypadku rzeczywiste obciążenie turbin wytwarzających ciepło, normalne i awaryjne tryby ich działania są uwzględniane w t-tym roku. Zgodnie z normami projektu technologicznego [48] rozważane są warunki awaryjne, w ramach których największa jednostka ulega awarii w elektrociepłowni. W tych warunkach należy zapewnić pełną satysfakcję konsumentów w zakresie ciepła dla celów technologicznych i pokrycie ogrzewania i krajowego obciążenia cieplnego w określonej wartości (około 60–70% maksimum), w zależności od warunków klimatycznych rozpatrywanego obszaru.
Zatem liczba energii, szczytowa para wodna i kotły z gorącą wodą są zwykle określane podczas normalnej pracy CHP, a następnie określane w warunkach awaryjnych. Liczbę kotłów energetycznych pierwszego rozmiaru (o większej wydajności jednostkowej lub wyższych parametrach początkowych pary), które należy wprowadzić do f-tego roku, oblicza się na podstawie rzeczywistego zużycia pary na turbinę pierwszego rozmiaru, liczby tych turbin (Z), nominalnej wydajność pary kotła i współczynnik uwzględniający zużycie pary na własne potrzeby elektrociepłowni kotłowej:

1) gdy zaawansowane turbiny wejściowe typu PT, gdy harmonogramy obciążenia technologicznego ciepła i zużycia ciepła w celu skompensowania utraty kondensatu produkcyjnego są pokryte (częściowo lub całkowicie) ciepłem, odpowiednio z pierwszego i drugiego wyboru:

Znaleziona wartość jest zaokrąglana do najbliższej większej liczby całkowitej, a gdy przybiera postać: 
Znaleziona liczba kotłów mocy, szczytowych i wodnych jest określona podczas awaryjnego działania CHP. Jednocześnie może okazać się wyższa niż w normalnych warunkach. W tym przypadku, przy określaniu dostaw ciepła z szczytowych kotłów parowych i nadwyżki ich mocy cieplnej, wychodzimy z ich największej liczby, biorąc pod uwagę, że szczytowe kotły parowe są ładowane jako pierwsze, a „rezerwa cieplna” koncentruje się na kotłach ciepłej wody.
Khrilev, LS, Smirnov, IA, Optymalizacja systemów ciepłowniczych i ciepłownictwa, Ed. E. Ya. Sokolova - M.: Energy, 1978.

